on computational aspects of tchebichef polynomials for higher polynomial order

On computational aspects of Tchebichef polynomials for higher polynomial order. SKTP is formed based on two existing hybrid OPs which are originated from Krawtchouk and Tchebichef polynomials.

The Normalized Charlier Polynomial Curves For Download Scientific Diagram

The calculation of the higher order polynomial base causes numerical instability seriously affecting the orthogonality property and the quality of the reconstruction.

. The presented method proposes a new initial value that does not tend to be zero as the polynomial size increases. Discrete orthogonal moments are utilized as a feature descriptor for images and video frames in computer vision applications. 31 and Zhu et al.

Results and comparison with other methods are presented. On the computational aspects of Charlier polynomials. Up to 10 cash back In this paper a new hybrid set of orthogonal polynomials OPs is presented.

On computational aspects of Krawtchouk polynomials for high orders. In this paper we present a new method for computing discrete Krawtchouk polynomial coefficients swiftly. Cogent Engineering 7 1 1763553 2020.

SH Abdulhussain AR Ramli SAR Al-Haddad BM Mahmmod WA Jassim. The second derivative of the Chebyshev polynomial of the first kind is which if evaluated as shown above poses a problem because it is indeterminate at x 1Since the function is a polynomial all of the derivatives must exist for all real numbers so the taking to limit on the expression above should yield the desired values taking the limit as x 1. In this work we propose a new algorithm for the computation of Tchebichef moments by means of a recurrence relation with respect to order and the GramSchmidt process which reduces the numerical instability and the carry error caused by the computation of high-order moments.

First the TPCs are computed for x n 0 1. In this paper we present a new method for computing discrete Krawtchouk polynomial coefficients swiftly and efficiently. Request PDF Some computational aspects of Tchebichef moments for higher orders In this work we propose a new algorithm for the computation of Tchebichef moments by means of a.

IEEE Access 5 1 2470-2478 2017. On Computational Aspects of Tchebichef Polynomials for Higher Polynomial Order View 2 peer reviews of On Computational Aspects of Tchebichef Polynomials for Higher Polynomial Order on Publons Download Web of Science My Research Assistant. SH Abdulhussain SAR Al-Haddad BM Mahmmod WA Jassim.

The new set of OPs is termed as squared KrawtchoukTchebichef polynomial SKTP. On Computational Aspects of Tchebichef Polynomials for Higher Polynomial Order Sadiq H. Even so the orthogonality of Tchebichef polynomials for higher orders is destroyed because of numerical approximation.

On Computational Aspects of Tchebichef Polynomials for Higher Polynomial Order. The mathematical design of the proposed OP is presented. Abdulhussain Abd Rahman Ramli Syed Abdul Rahman Al-Haddad Basheera M.

The major issue of CHPs is the numerical instability of coefficients for high-order polynomials. Fast and stable computation of higher-order Hahn polynomials and Hahn moment invariants for signal and image analysis. Abdulhussain ORCiD Department of Computer and Communication Systems Engineering Universiti Putra Malaysia Selangor Malaysia.

Fast Recursive Computation of Krawtchouk Polynomials. Rahman Ramli Syed Abdul Rahman Al-Haddad Basheera M. Finally a new symmetry relation for CHPs is realized.

Abstract Charlier polynomials CHPs and their moments are commonly used in image processing due to their salient performance in the analysis of signals and their capability in signal representation. In this paper a new algorithm is proposed to compute the TP coefficients TPCs for higher polynomial order by combining two existing recurrence algorithms. Up to 10 cash back Tchebichef moments use the Tchebichef polynomials as the kernel.

18 discuss some computational aspects of Tchebichef polynomials and moments such as symmetry property polynomial expansion and recurrence relations with respect to n and x. However one problem encountered in the calculation of high-order polynomial values is the propagation of numerical er-. 32 propose to use recurrence relationships to reduce numerical.

Tchebichef polynomials TPs and their moments are widely used in signal processing due to their remarkable performance in signal analysis feature extraction and. On Computational Aspects of Tchebichef Polynomials for Higher Polynomial Order. On computational aspects of Tchebichef polynomials for higher polynomial order.

First sufficient initial values are obtained mathematically. N2 - 1 using the recurrence in the x-direction. Full PDF Package Download Full PDF Package.

In this work we propose a new algorithm for the computation of Tchebichef moments by means of a recurrence relation with respect to order and the Gram-Schmidt process which reduces. Enter the email address you signed up with and well email you a reset link. A solution can be devised to eliminate the carry error to compute high-order polynomials through the GramSchmidt process.

Multimedia Tools and Applications. Discrete Krawtchouk polynomials are widely utilized in different fields for their remarkable characteristics specifically the localization property. This problem severely affects the quality of image reconstruction particularly in high resolution images.

The proposed algorithm makes the computation of the TP superior to that of conventional recurrence algorithms when the polynomial order is large and also accelerates the computational speed of the TPCs. Abstract The computation of high-order discrete orthogonal moments is very complex and unstable due to fluctuations in numerical polynomial values. In addition a combination of the existing recurrence relations is presented which are in the n- and x-directions.

In this study a new recurrence algorithm is proposed to generate CHPs for high-order polynomials. The three-term recurrence relations in the n-direction and x-direction. Bring the power of the Web of Science to your mobile device wherever inspiration strikes.

Instability of coefficients for high-order polynomials. BM Mahmmod AM Abdul-Hadi SH. Second the reduced form of the recur- rence algorithm is determined.

In this study a new recurrence algorithm is proposed to generate CHPs for high.

2

Orthogonal Polynomials Plots For Different Values Of Polynomial Order N Download Scientific Diagram

Orthogonal Polynomials Plots For Different Values Of Polynomial Order N Download Scientific Diagram

Mhamed Sayyouri Laboratoire D Ingenierie Systemes Et Applications Lisa Professor Sidi Mohamed Ben Abdellah University Fes

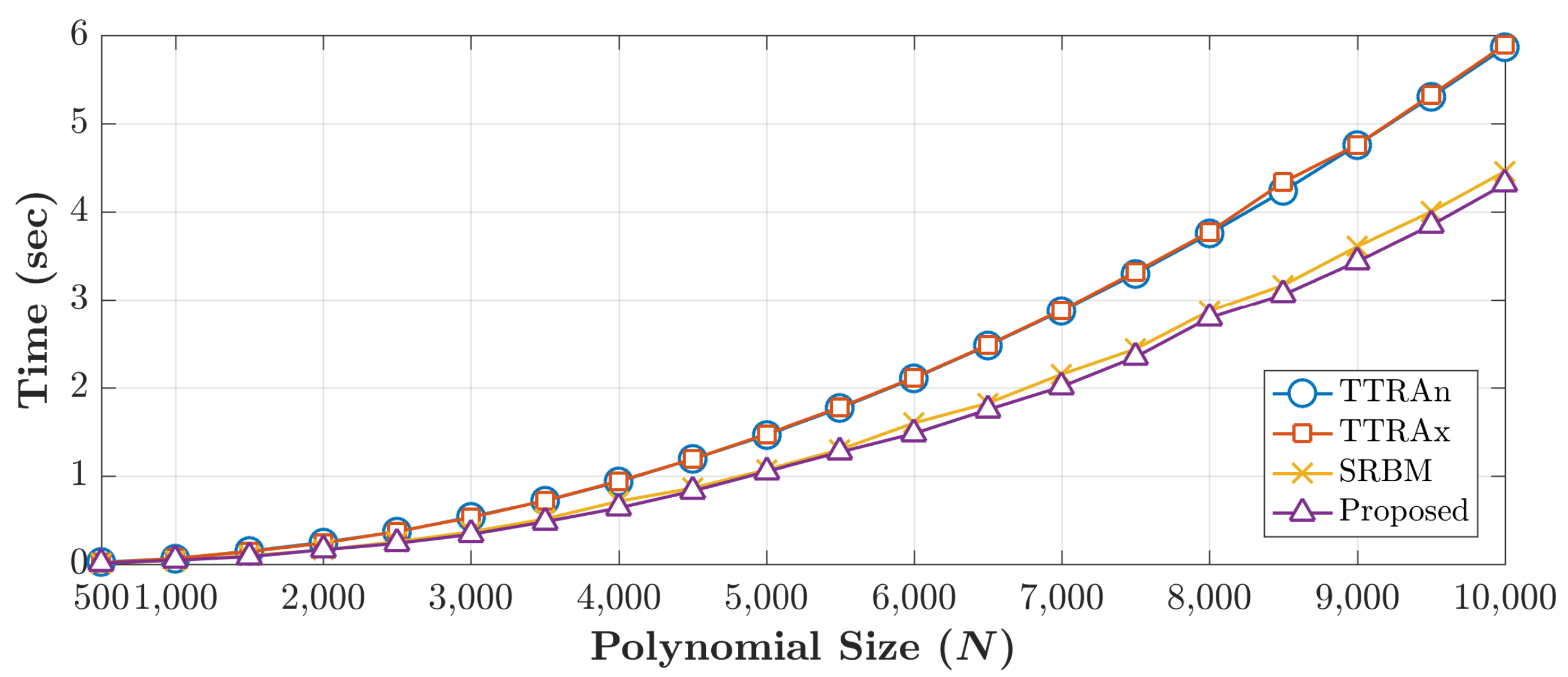
J Imaging Free Full Text On Computational Aspects Of Krawtchouk Polynomials For High Orders Html

Plot Of K 0 5 0 X For Different Values Of Polynomial Size Download Scientific Diagram

Plot Of K 0 5 0 X For Different Values Of Polynomial Size Download Scientific Diagram

2

On Computational Aspects Of High Order Dual Hahn Moments Sciencedirect

The Normalized Charlier Polynomial Curves For Download Scientific Diagram

On Computational Aspects Of High Order Dual Hahn Moments Sciencedirect

On Computational Aspects Of High Order Dual Hahn Moments Sciencedirect

2

On Computational Aspects Of High Order Dual Hahn Moments Sciencedirect

Comparison Of The Llr Quality Measure For Different Speech Enhancement Download Scientific Diagram

On Computational Aspects Of High Order Dual Hahn Moments Sciencedirect

On Computational Aspects Of High Order Dual Hahn Moments Sciencedirect

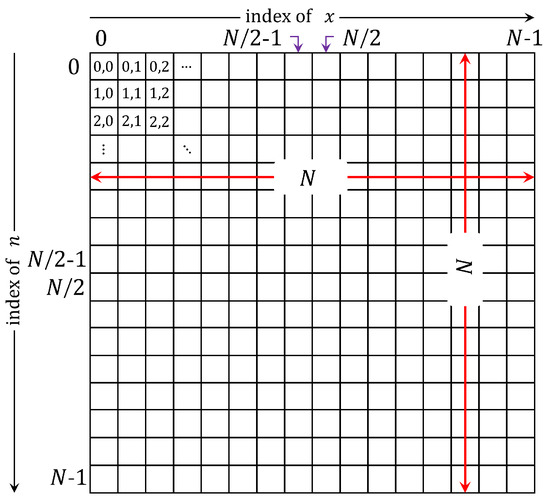
J Imaging Free Full Text On Computational Aspects Of Krawtchouk Polynomials For High Orders Html

Orthogonal Polynomials Plots For Different Values Of Polynomial Order N Download Scientific Diagram